理解向量
| 本站(springdoc.cn)中的内容来源于 spring.io ，原始版权归属于 spring.io。由 springdoc.cn 进行翻译，整理。可供个人学习、研究，未经许可，不得进行任何转载、商用或与之相关的行为。 商标声明：Spring 是 Pivotal Software, Inc. 在美国以及其他国家的商标。 |
向量具有维度和方向。例如，下图描绘了笛卡尔坐标系中的二维向量 ，以箭头形式呈现。
向量 的头部位于点 。x 坐标值为 ，y 坐标值为 。这些坐标也被称为向量的分量。
相似性
有多种数学公式可用于判断两个向量是否相似。其中最直观易懂的是余弦相似度。请看以下展示三组图形的图像：
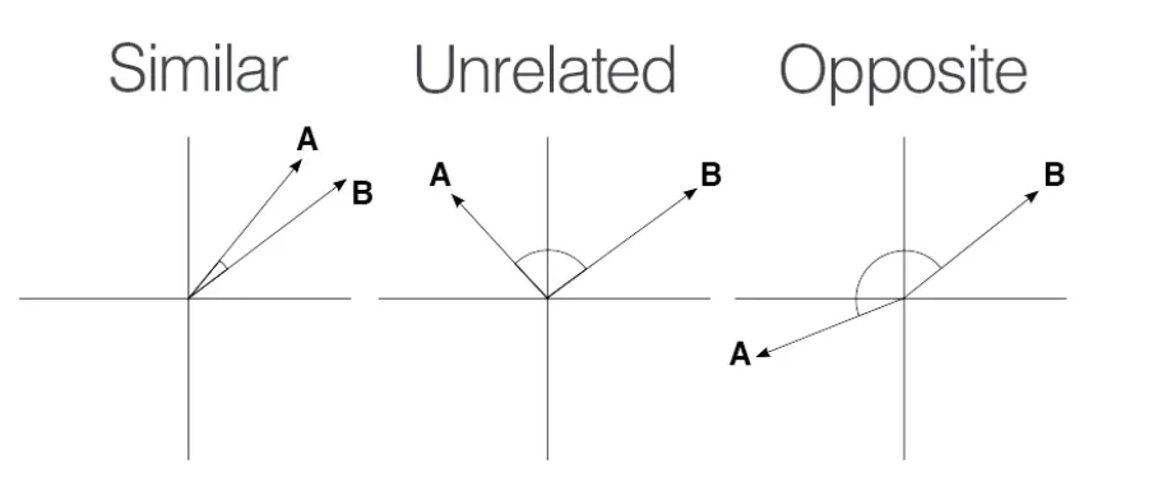
当向量 和 指向相近方向时（如第一张图所示），它们被认为是相似的。当向量互相垂直时被视为不相关，而方向相反时则被视为对立。
它们之间的夹角 是衡量相似度的有效指标。如何计算角度 呢？
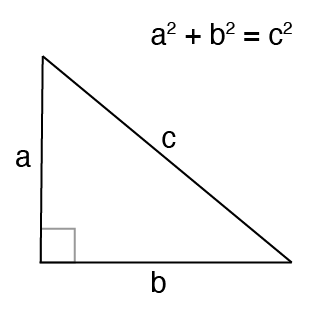
我们都熟悉 勾股定理。
当向量 a 和 b 之间的夹角不是 90 度时该怎么办？
这时就需要用到 余弦定理。
下图以向量图形式展示了这种方法：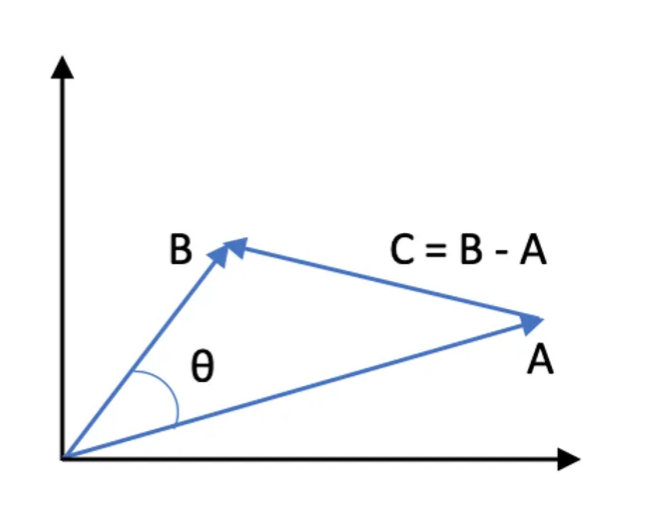
该向量的大小（或长度、模）根据其分量定义为：
两个向量 和 的点积根据其分量定义为：
用向量大小和点积重写余弦定律可以得到以下结果：
将 替换为 ，得到如下公式：
该公式适用于二维或三维以上的高维空间，尽管难以直观可视化。不过，在一定程度上仍然可以进行可视化。在人工智能和机器学习应用中，向量通常具有数百甚至数千个维度，这是很常见的。
下面展示了在高维空间中使用向量分量的相似性函数。它通过使用 求和（Summation）数学符号，将之前给出的二维情况下的模和点积定义扩展到 N 维空间。
这是在简单实现向量存储时使用的关键公式，你可以在 SimpleVectorStore 的实现中找到它。
